神秘的牛吃草问题
牛吃草问题广泛存在于行测考试数学运算部分的题目中,对于这一问题,许多同学往往会感到题目理解比较困难,花费的时间很多,但是真正能够解决的牛吃草问题很少,甚至干脆放弃这部分题目。今天江苏公务员考试网就带大家一起,揭开牛吃草问题的神秘面纱,掌握做题思路,化繁为简。
例题展示
①一片牧场上的青草每天匀速生长,牧场上的草如果28头牛可以吃6天,如果21头牛吃可以吃9天。那么牧场上的青草可供13头牛吃几天?
②由于天气逐渐变冷,牧场上的草每天以均匀的速度减少。经计算,牧场上的草如果6头牛吃可以吃12天,如果8头牛吃可以吃10天。那么牧场上的青草可供11头牛吃几天?
题目特征总结
通过以上两到例题,我们可以将牛吃草问题的题目特征进行总结:
特点(一):原有草量是固定的;草量受两个因素制约:一是草每天匀速生长(减少),使草量增加(减少),二是牛吃草使草量减少;
特点(二):题目中大量使用排比句式:如果……如果……。
因此满足以上两种特征的题目,我们就可以将其归类为牛吃草问题。
题型分类
牛吃草问题可以大体分为三类题型即:夏天(追及)型牛吃草,冬天(相遇)型牛吃草,极值型牛吃草。今天我们主要学习第一类。
解题思维及方法精析
对于夏天型牛吃草问题,我们可以从上文提到的例题一入手。可以把草原想象成一条线段,所有的牛排成一列沿着草原线段的左边端点开始向右侧吃草,生长的草是从草原线段的右端点统一向右生长,此时可以相当于牛和草两个运动物体,以草原线段为初始距离,展开一场追及过程,因此就可以利用追及公式,将该模型进行转化。具体如下:
将草原原有草量设为M,将草生长速度设为x,每头牛单位时间吃草的量为1,数量为N,吃草的时间为t,则夏天型牛吃草的公式就可以总结为:
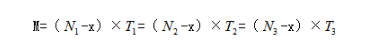
后续做题中我们只需要将题目中所给的数据带入到以上式子中即可。
试题精析
例1
一片牧场上的青草每天匀速生长,牧场上的草如果28头牛可以吃6天,如果21头牛吃可以吃9天。那么牧场上的青草可供13头牛吃几天?
【解析】:假设可供13头牛吃t天,则有M=(28-x)×6=(21-x)×9=(13-x)×t,解得 x=7,M=126,t=21,故可供13 头牛吃21天。
例2
省博物馆每日9点开馆,有大量观众前来参观,很早就有人排队等候入场,假设从第一个观众到来起,每分钟来的观众人数一样多,每个入场口进入的速度是一样的,如果开放5个入场口,则9点20分就不再有人排队,如果设6个入场口,则9点15分就没有人排队,那么第一个观众到达时间是:
A.9 时 B.8 时 45 分
C.8 时 30 分 D.8 时 15 分
【解析】:假设每个入场口每分钟只能进1人,每分钟来的观众数为x人,则有(5-x)×20=(6-x)×15,解得x=2人,九点时到场观众数(5-2)×20=60人,60÷2=30分钟,故第一个观众到达时间是8时30分。选 C。
 相关文章
相关文章



